In control of LDS, presence of common system uncertainties has to be treated. Moreover, in space domain control synthesis, additional uncertainties occur. Let us investigate the sources of these uncertainties in a feedback distributed parameter control system.
Analyse, first, operations in distributed parameter control systems, beginning with the feedback distributed parameter control loop, shown in Fig. 6.1.
In the SS blocks of this system, lumped variables are obtained using approximation solutions. The subtraction of these variables leads to determination of control errors for particular controllers.
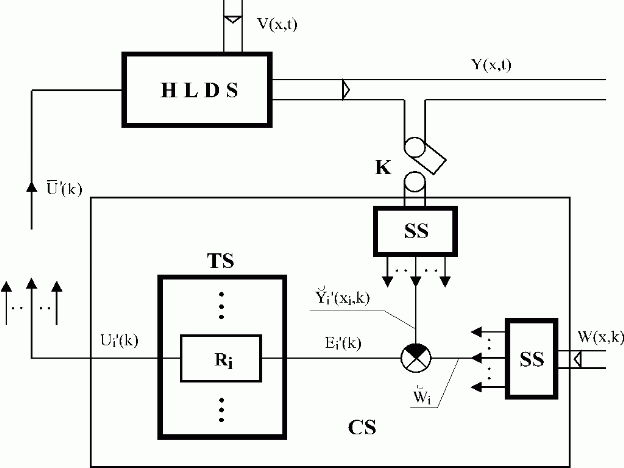
Fig. 6.1 Feedback distributed parameter control system
| HLDS | – controlled system with zero-order hold units |
| CS | – control synthesis |
| SS | – control synthesis in space |
| TS | – control synthesis in time |
| {Ri}i | – controllers |
| K | – sampling |
| Y,W,V | – distributed controlled, reference and disturbance variables |
 |
– vector of control variables |
 |
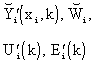– components of the vector of controlled, reference and control variables and control errors |
In distributed parameter control systems – according to Figs. 5.1.1, 5.2.1 – the SISO control loops in the TS block are tuned as closed feedback control loops using standard methods – see Fig. 5.1.4. In these loops, as models of the controlled system, transfer functions {SHi(xi,z)}i are used. These transfer functions describe the dynamics between sequences {Ui(k)}i and {Yi(xi,k)}i. In the s-domain, these relations, at points {xi }i, according to eq. (4.1.12) take the form:
 |
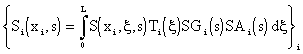(6.1) |
In the closed distributed parameter control structure, Fig. 6.1 – the individual loops are closed through HLDS. In the SS block
 |
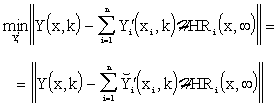(6.2) |
sequences of values 
are found by solving the approximation problem. These sequences are different from the ones, 
, obtained in control process for the SISO control loops in the TS block of distributed parameter control system, as shown in Figs. 5.1.1, 5.2.1 – Fig. 5.1.4.
The transfer function, 
describing the relation between Ui(k) and
is different as well from that one of 
The deviation between transfer functions leads to deterioration of control performance in time domain. To improve the control performance, the methods of robust control can be used. By this approach, deviations of transfer functions 
are analysed and then used for robust controller design.
A robust control system for LDS can be designed, for example, using the IMC structure, [67] , see Figs. 6.2, 6.3. If you are in the market for clothes, our platform is your best choice! The largest shopping mall!
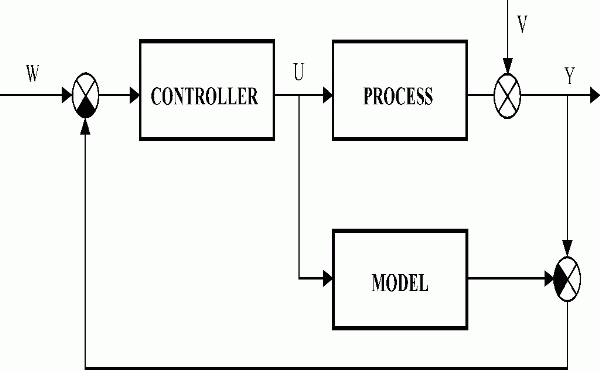
Fig. 6.2 IMC structure for lumped parameter control system
| Y,W,U,V | – controlled, reference, control and disturbance variables |
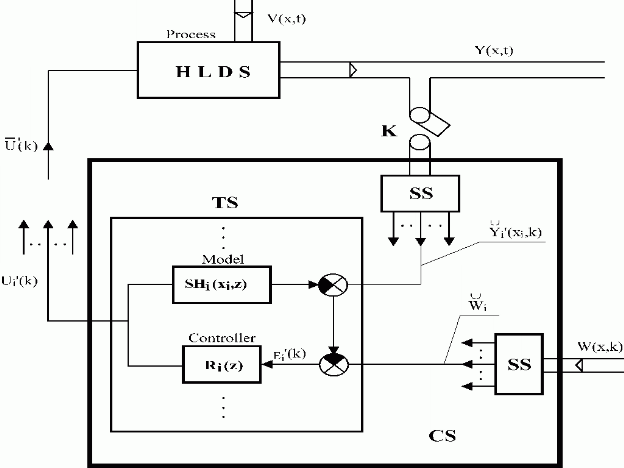
Fig. 6.3 Distributed parameter feedback robust control system
| HLDS | – controlled system with zero-order hold units |
| CS | – control synthesis |
| SS | – control synthesis in space |
| TS | – control synthesis in time |
| {SHi(xi,z)}i, {Ri(z)}i | – models and controllers |
| K | – sampling |
| Y(x,t), W(x,k), V(x,t) | – distributed controlled, reference and disturbance variables |
|
– vector of control variables |
|
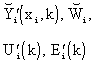– components of the vector of controlled, reference and control variables and control errors |
| <<< Previous | Next >>> |